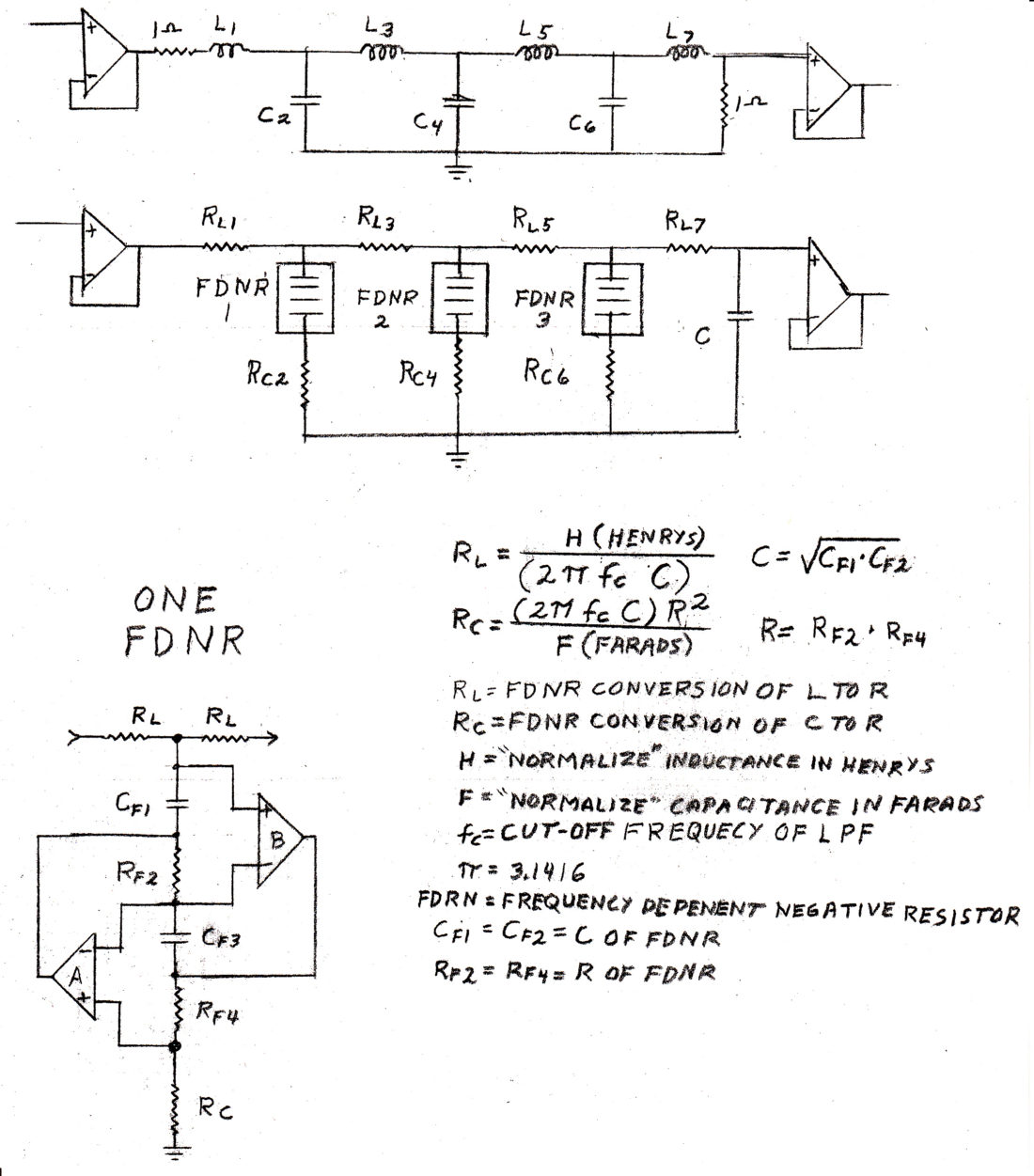


The following formulas can be used to convert a normalized low pass filter design to a FDNR configuration that converts two normalized series inductance and one shunt normalized capacitance through the FDNR conversion process to resistors that simulate the same inductances and capacitances required by the Normalized Low Pass Filter for each FDNR section. Additional sections may be added if a sharper cut off is required. For instance, a seven element low pass filter may be constructed with three FDNR sections that require six FDNR operational amplifiers plus the zero source impedance operational amplifier at the input and high impedance converter operational amplifier at the output for a total of eight operational amplifiers.
Rc = 2 * PIE * Fc * Cfdnr * Rfdnr * Rfdnr = Resistance value that transforms to Capacity.
Rl = Henrys_____ = Resistance value that transforms to Inductance.
. 2 * PIE * Fc * Cfdnr
The FDNR internal components must be high quality, temperature stable value components, preferably of 1% accuracy. All of the internal capacitors are of the exact same value, and so are the internal resistors.
Rfdnr = R2, = R4 = 1000 Ohms 1%
Cfdnr = C1, C3, Ct = 0.01 Micro Farad temperature stable capacitors, 1%. , or trim with parallel Capacitors to achieve correct value. This particular value of capacity is used because the Reactance of 0.01 microfarads equals 1000 ohms at 15,000 Hz, thus making Rc and Rl Equal at the cut off frequency. This makes Rfdnr = Cfdnr reactance at cut off frequency.
Fc = Cut-off frequency of LPF (Low Pass Filter).
When the suggested FDNR internal components are used to implement the FDNR, then the following formulas may be used.
Rc (2, 4 , 6) = 2 * PIE * Fc * 0.01 = Resistance value that transforms to Capacity.
. Farads (F2, F4, F6)
Rl(1, 3, 5, 7, ) = _ Henrys_* 100,000,000 _ = Resistance value that transforms to Inductance.
. 2 * PIE * Fc (H1, H3, H5. H7)
THE FOLLOWING FORMULAS ASSUME (TWO) 0.01 MICROFARAD CAPACITORS AND (TWO) 1000 OHM RESISTORS IN EACH FDNR NETWORK.
Rc = 0.0628319 * Fc_
Rl = 15.9155 * 10 * Henries